7 Normalization

7.1 Normalization

Normalization is a method where we modify a variable by subtracting the mean and dividing by the standard deviation

\[X_{scaled} = \dfrac{X - \text{mean}(X)}{\text{sd}(X)}\]

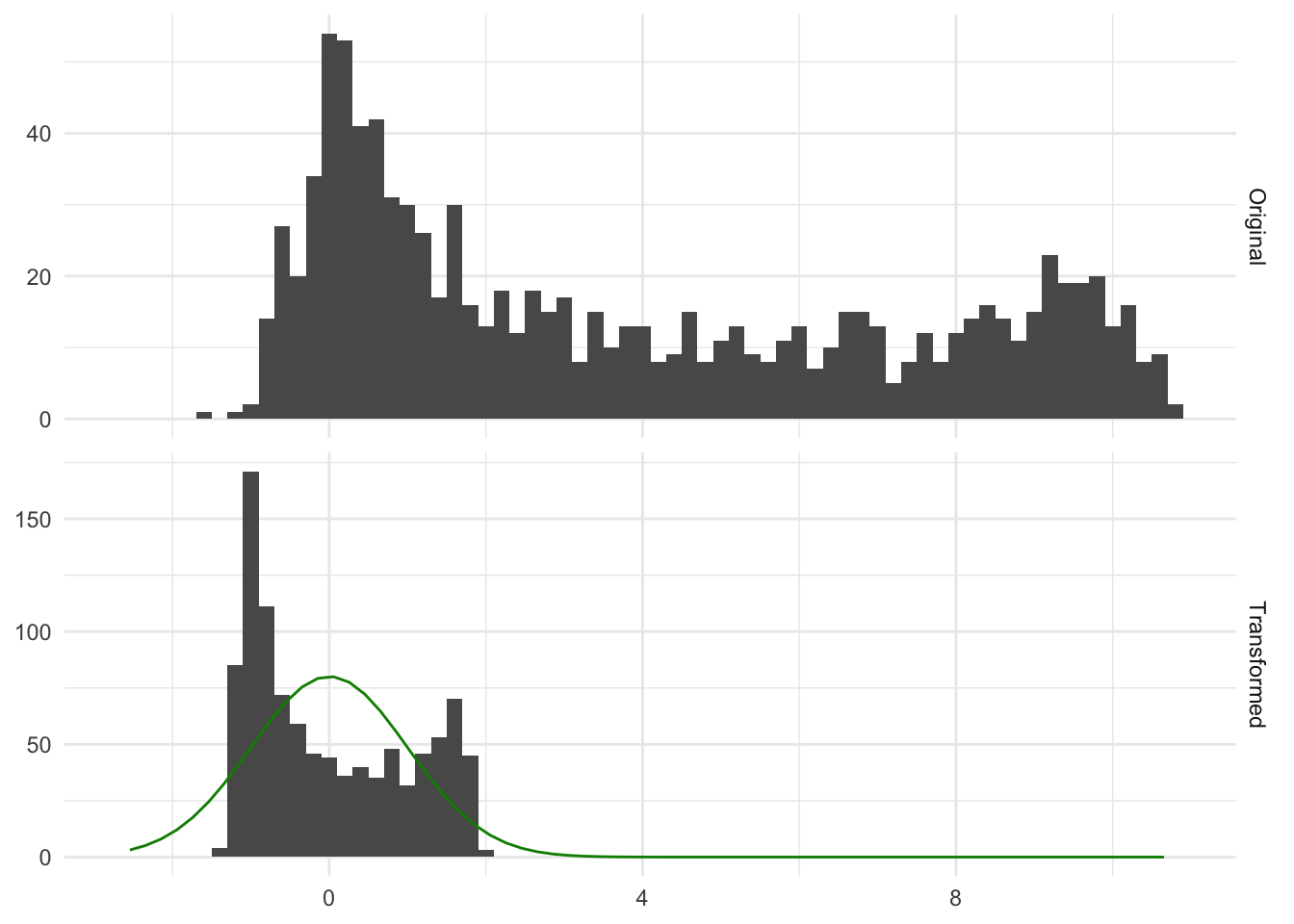
Performing this transformation means that the resulting variable will have a mean of 0 and a standard deviation and variance of 1. This method is a learned transformation. So we use the training data to derive the right values of \(\text{sd}(X)\) and \(\text{mean}(X)\) and then these values are used to perform the transformations when applied to new data. It is a common misconception that this transformation is done to make the data normally distributed. This transformation doesn’t change the distribution, it scales the values. Below is a figure Figure 7.1 that illustrates that point

2 histograms of distribution one above the other. The top distribution shows a bimodal distribution. Below is the same distribution after being normalized. Both appear clearly non-normally distributed. The green curve is overlaid lower histogram. It doesn't follow. — Figure 7.1: Normalization doesn’t make data more normal. The green curve indicates the density of the unit normal distribution.

In Figure 7.1 we see some distribution, before and after applying normalization to it. Both the original and transformed distribution are bimodal, and the transformed distribution is no more normal than the original. That is fine because the transformation did its job by moving the values close to 0 and a specific spread, which in this case is a variance of 1.

7.2 Pros and Cons

7.2.1 Pros

If you don’t have any severe outliers then you will rarely see any downsides to applying normalization
Fast calculations
Transformation can easily be reversed, making its interpretations easier on the original scale

7.2.2 Cons

Not all software solutions will be helpful when applying this transformation to a constant variable. You will often get a “division by 0” error
Cannot be used with sparse data as it isn’t preserved because of the centering that is happening. If you only scale the data you don’t have a problem
This transformation is highly affected by outliers, as they affect the mean and standard deviation quite a lot

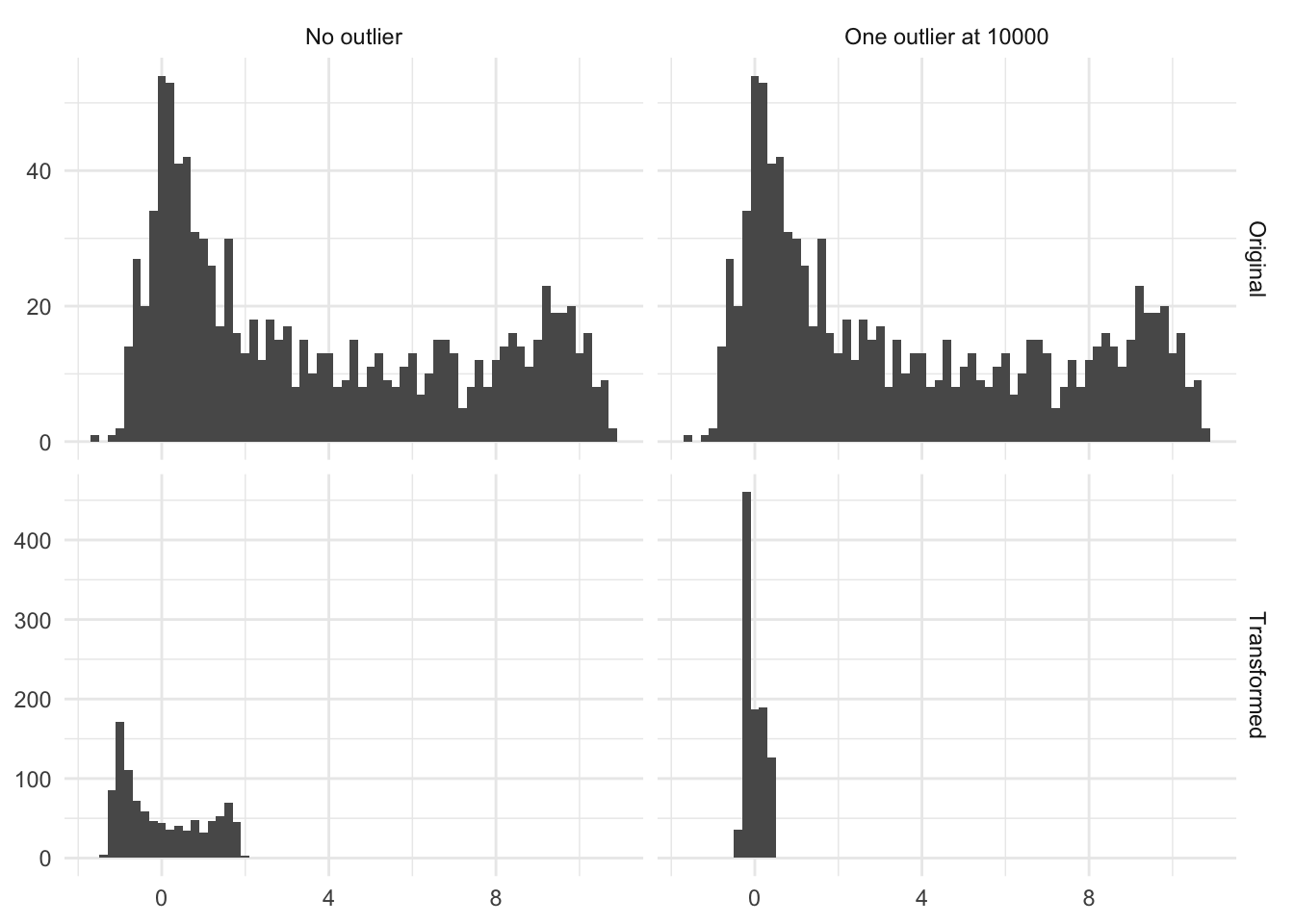
Below is the figure Figure 7.2 is an illustration of the effect of having a single high value. In this case, a single observation with the value 10000 moved the transformed distribution much tighter around zero. And all but removed the variance of the non-outliers.

4 histograms of distribution in 2 columns. The top distribution shows the same bimodal distribution. Below are the same distributions after being normalized. The right column shows the effect of having one outlier at 10000, which in this case made the transformed distribution about a fifth of the width. — Figure 7.2: Outliers can have a big effect on the resulting distribution when applying normalization.

7.3 R Examples

We will be using the ames data set for these examples.

library(recipes)
library(modeldata)
data("ames")

ames |>
  select(Sale_Price, Lot_Area, Wood_Deck_SF, Mas_Vnr_Area)

# A tibble: 2,930 × 4
   Sale_Price Lot_Area Wood_Deck_SF Mas_Vnr_Area
        <int>    <int>        <int>        <dbl>
 1     215000    31770          210          112
 2     105000    11622          140            0
 3     172000    14267          393          108
 4     244000    11160            0            0
 5     189900    13830          212            0
 6     195500     9978          360           20
 7     213500     4920            0            0
 8     191500     5005            0            0
 9     236500     5389          237            0
10     189000     7500          140            0
# ℹ 2,920 more rows

{recipes} provides a step to perform scaling, centering, and normalization. They are called step_scale(), step_center() and step_normalize() respectively.

Below is an example using step_scale()

scale_rec <- recipe(Sale_Price ~ ., data = ames) |>
  step_scale(all_numeric_predictors()) |>
  prep()

scale_rec |>
  bake(new_data = NULL, Sale_Price, Lot_Area, Wood_Deck_SF, Mas_Vnr_Area)

# A tibble: 2,930 × 4
   Sale_Price Lot_Area Wood_Deck_SF Mas_Vnr_Area
        <int>    <dbl>        <dbl>        <dbl>
 1     215000    4.03          1.66        0.627
 2     105000    1.47          1.11        0    
 3     172000    1.81          3.11        0.605
 4     244000    1.42          0           0    
 5     189900    1.76          1.68        0    
 6     195500    1.27          2.85        0.112
 7     213500    0.624         0           0    
 8     191500    0.635         0           0    
 9     236500    0.684         1.88        0    
10     189000    0.952         1.11        0    
# ℹ 2,920 more rows

We can also pull out the value of the standard deviation for each variable that was affected using tidy()

scale_rec |>
  tidy(1)

# A tibble: 33 × 3
   terms            value id         
   <chr>            <dbl> <chr>      
 1 Lot_Frontage     33.5  scale_FGmgk
 2 Lot_Area       7880.   scale_FGmgk
 3 Year_Built       30.2  scale_FGmgk
 4 Year_Remod_Add   20.9  scale_FGmgk
 5 Mas_Vnr_Area    179.   scale_FGmgk
 6 BsmtFin_SF_1      2.23 scale_FGmgk
 7 BsmtFin_SF_2    169.   scale_FGmgk
 8 Bsmt_Unf_SF     440.   scale_FGmgk
 9 Total_Bsmt_SF   441.   scale_FGmgk
10 First_Flr_SF    392.   scale_FGmgk
# ℹ 23 more rows

We could also have used step_center() and step_scale() together in one recipe

center_scale_rec <- recipe(Sale_Price ~ ., data = ames) |>
  step_center(all_numeric_predictors()) |>
  step_scale(all_numeric_predictors()) |>
  prep()

center_scale_rec |>
  bake(new_data = NULL, Sale_Price, Lot_Area, Wood_Deck_SF, Mas_Vnr_Area)

# A tibble: 2,930 × 4
   Sale_Price Lot_Area Wood_Deck_SF Mas_Vnr_Area
        <int>    <dbl>        <dbl>        <dbl>
 1     215000   2.74          0.920       0.0610
 2     105000   0.187         0.366      -0.566 
 3     172000   0.523         2.37        0.0386
 4     244000   0.128        -0.742      -0.566 
 5     189900   0.467         0.936      -0.566 
 6     195500  -0.0216        2.11       -0.454 
 7     213500  -0.663        -0.742      -0.566 
 8     191500  -0.653        -0.742      -0.566 
 9     236500  -0.604         1.13       -0.566 
10     189000  -0.336         0.366      -0.566 
# ℹ 2,920 more rows

Using tidy() we can see information about each step

center_scale_rec |>
  tidy()

# A tibble: 2 × 6
  number operation type   trained skip  id          
   <int> <chr>     <chr>  <lgl>   <lgl> <chr>       
1      1 step      center TRUE    FALSE center_tSRk5
2      2 step      scale  TRUE    FALSE scale_kjP2v

And we can pull out the means using tidy(1)

center_scale_rec |>
  tidy(1)

# A tibble: 33 × 3
   terms             value id          
   <chr>             <dbl> <chr>       
 1 Lot_Frontage      57.6  center_tSRk5
 2 Lot_Area       10148.   center_tSRk5
 3 Year_Built      1971.   center_tSRk5
 4 Year_Remod_Add  1984.   center_tSRk5
 5 Mas_Vnr_Area     101.   center_tSRk5
 6 BsmtFin_SF_1       4.18 center_tSRk5
 7 BsmtFin_SF_2      49.7  center_tSRk5
 8 Bsmt_Unf_SF      559.   center_tSRk5
 9 Total_Bsmt_SF   1051.   center_tSRk5
10 First_Flr_SF    1160.   center_tSRk5
# ℹ 23 more rows

and the standard deviation using tidy(2)

center_scale_rec |>
  tidy(2)

# A tibble: 33 × 3
   terms            value id         
   <chr>            <dbl> <chr>      
 1 Lot_Frontage     33.5  scale_kjP2v
 2 Lot_Area       7880.   scale_kjP2v
 3 Year_Built       30.2  scale_kjP2v
 4 Year_Remod_Add   20.9  scale_kjP2v
 5 Mas_Vnr_Area    179.   scale_kjP2v
 6 BsmtFin_SF_1      2.23 scale_kjP2v
 7 BsmtFin_SF_2    169.   scale_kjP2v
 8 Bsmt_Unf_SF     440.   scale_kjP2v
 9 Total_Bsmt_SF   441.   scale_kjP2v
10 First_Flr_SF    392.   scale_kjP2v
# ℹ 23 more rows

Since these steps often follow each other, we often use the step_normalize() as a shortcut to do both operations in one step

scale_rec <- recipe(Sale_Price ~ ., data = ames) |>
  step_normalize(all_numeric_predictors()) |>
  prep()

scale_rec |>
  bake(new_data = NULL, Sale_Price, Lot_Area, Wood_Deck_SF, Mas_Vnr_Area)

# A tibble: 2,930 × 4
   Sale_Price Lot_Area Wood_Deck_SF Mas_Vnr_Area
        <int>    <dbl>        <dbl>        <dbl>
 1     215000   2.74          0.920       0.0610
 2     105000   0.187         0.366      -0.566 
 3     172000   0.523         2.37        0.0386
 4     244000   0.128        -0.742      -0.566 
 5     189900   0.467         0.936      -0.566 
 6     195500  -0.0216        2.11       -0.454 
 7     213500  -0.663        -0.742      -0.566 
 8     191500  -0.653        -0.742      -0.566 
 9     236500  -0.604         1.13       -0.566 
10     189000  -0.336         0.366      -0.566 
# ℹ 2,920 more rows

And we can still pull out the means and standard deviations using tidy()

scale_rec |>
  tidy(1) |>
  filter(terms %in% c("Lot_Area", "Wood_Deck_SF", "Mas_Vnr_Area"))

# A tibble: 6 × 4
  terms        statistic   value id             
  <chr>        <chr>       <dbl> <chr>          
1 Lot_Area     mean      10148.  normalize_ucdPw
2 Mas_Vnr_Area mean        101.  normalize_ucdPw
3 Wood_Deck_SF mean         93.8 normalize_ucdPw
4 Lot_Area     sd         7880.  normalize_ucdPw
5 Mas_Vnr_Area sd          179.  normalize_ucdPw
6 Wood_Deck_SF sd          126.  normalize_ucdPw

7.4 Python Examples

We are using the ames data set for examples. {sklearn} provided the StandardScaler() method we can use. By default we can use this method to perform both the centering and scaling.

from feazdata import ames
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import StandardScaler

ct = ColumnTransformer(
    [('normalize', StandardScaler(), ['Sale_Price', 'Lot_Area', 'Wood_Deck_SF',  'Mas_Vnr_Area'])], 
    remainder="passthrough")

ct.fit(ames)

ColumnTransformer(remainder='passthrough',
                  transformers=[('normalize', StandardScaler(),
                                 ['Sale_Price', 'Lot_Area', 'Wood_Deck_SF',
                                  'Mas_Vnr_Area'])])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

ct.transform(ames)

      normalize__Sale_Price  ...  remainder__Latitude
0                     0.428  ...               42.054
1                    -0.949  ...               42.053
2                    -0.110  ...               42.053
3                     0.791  ...               42.051
4                     0.114  ...               42.061
...                     ...  ...                  ...
2925                 -0.479  ...               41.989
2926                 -0.623  ...               41.988
2927                 -0.611  ...               41.987
2928                 -0.135  ...               41.991
2929                  0.090  ...               41.989

[2930 rows x 74 columns]

To only perform scaling, you set with_mean=False.

ct = ColumnTransformer(
    [('scaling', StandardScaler(with_mean=False, with_std=True), ['Sale_Price', 'Lot_Area', 'Wood_Deck_SF',  'Mas_Vnr_Area'])], 
    remainder="passthrough")

ct.fit(ames)

ColumnTransformer(remainder='passthrough',
                  transformers=[('scaling', StandardScaler(with_mean=False),
                                 ['Sale_Price', 'Lot_Area', 'Wood_Deck_SF',
                                  'Mas_Vnr_Area'])])

ct.transform(ames)

      scaling__Sale_Price  ...  remainder__Latitude
0                   2.692  ...               42.054
1                   1.315  ...               42.053
2                   2.153  ...               42.053
3                   3.055  ...               42.051
4                   2.378  ...               42.061
...                   ...  ...                  ...
2925                1.784  ...               41.989
2926                1.640  ...               41.988
2927                1.653  ...               41.987
2928                2.128  ...               41.991
2929                2.354  ...               41.989

[2930 rows x 74 columns]

And to only perform centering you set with_mean=True.

ct = ColumnTransformer(
    [('centering', StandardScaler(with_mean=True, with_std=False), ['Sale_Price', 'Lot_Area', 'Wood_Deck_SF',  'Mas_Vnr_Area'])], 
    remainder="passthrough")

ct.fit(ames)

ColumnTransformer(remainder='passthrough',
                  transformers=[('centering', StandardScaler(with_std=False),
                                 ['Sale_Price', 'Lot_Area', 'Wood_Deck_SF',
                                  'Mas_Vnr_Area'])])

ct.transform(ames)

      centering__Sale_Price  ...  remainder__Latitude
0                  34203.94  ...               42.054
1                 -75796.06  ...               42.053
2                  -8796.06  ...               42.053
3                  63203.94  ...               42.051
4                   9103.94  ...               42.061
...                     ...  ...                  ...
2925              -38296.06  ...               41.989
2926              -49796.06  ...               41.988
2927              -48796.06  ...               41.987
2928              -10796.06  ...               41.991
2929                7203.94  ...               41.989

[2930 rows x 74 columns]